Probabilidad condicional es la probabilidad de que ocurra un evento A, sabiendo que también sucede otro evento B. La probabilidad condicional se escribe P(A|B), y se lee «la probabilidad de A dado B».
No tiene por qué haber una relación causal o temporal entre A y B. A puede preceder en el tiempo a B, sucederlo o pueden ocurrir simultáneamente. A puede causar B,
viceversa o pueden no tener relación causal. Las relaciones causales o
temporales son nociones que no pertenecen al ámbito de la probabilidad.
Pueden desempeñar un papel o no dependiendo de la interpretación que se
le dé a los eventos.
El condicionamiento de probabilidades puede lograrse aplicando el teorema de Bayes:
Resulta que:
Las probabilidades p(A1) se denominan probabilidades a priori.
Las probabilidades p(Ai/B) se denominan probabilidades a posteriori.
Las probabilidades p(B/Ai) se denominan verosimilitudes.
Ejemplos
1.-El 20% de los empleados de una empresa son
ingenieros y otro 20% son economistas. El 75% de los ingenieros ocupan
un puesto directivo y el 50% de los economistas también, mientras que
los no ingenieros y los no economistas solamente el 20% ocupa un puesto
directivo. ¿Cuál es la probabilidad de que un empleado directivo elegido
al azar sea ingeniero?

2.-La probabilidad de que
haya un accidente en una fábrica que dispone de alarma es 0.1. La
probabilidad de que suene esta sí se ha producido algún incidente es de
0.97 y la probabilidad de que suene si no ha sucedido ningún incidente
es 0.02.
En el supuesto de que haya funcionado la alarma, ¿cuál es la probabilidad de que no haya habido ningún incidente?
Sean los sucesos:
I = Producirse incidente.
A = Sonar la alarma.

a. Determine el valor de la probabilidad de que sea menor de 24 meses.
b. Si el infante resulta ser menor de 24 meses. Determine la probabilidad que sea una niña.
SOLUCIÓN:
Se definen los sucesos:
Suceso H: seleccionar una niña.
Suceso V: seleccionar un niño.
Suceso M: infante menor de 24 meses.
En los ejercicios de probabilidad total y teorema de bayes, es importante identificar los sucesos que forman la población y cuál es la característica que tienen en común dichos sucesos. Estos serán los sucesos condicionados.
a. En este caso, la población es de los infantes. Y la característica en común es que sean menores de 24 meses. Por lo tanto, la probabilidad de seleccionar un infante menor de 24 meses es un ejemplo de probabilidad total. Su probabilidad será:
b. Para identificar cuando en un ejercicio se hace referencia al teorema de bayes, hay que partir de reconocer esta es una probabilidad condicionada y que la característica común de los sucesos condicionantes ya ha ocurrido. Entonces, la probabilidad de que sea niña una infante menor de 24 meses será:
4.-Un médico cirujano se especializa en cirugías estéticas. Entre sus pacientes, el 20% se realizan correcciones faciales, un 35% implantes mamarios y el restante en otras cirugías correctivas. Se sabe además, que son de genero masculino el 25% de los que se realizan correcciones faciales, 15% implantes mamarios y 40% otras cirugías correctivas. Si se selecciona un paciente al azar, determine:
a. Determine la probabilidad de que sea de género masculino
b. Si resulta que es de género masculino, determine la probabilidad que se haya realizado una cirugía de implantes mamarios.
SOLUCIÓN:
Se definen los sucesos:
Suceso F: pacientes que se realizan cirugías faciales
Suceso M: pacientes que se realizan implantes mamarios
Suceso O: pacientes que se realizan otras cirugías correctivas
Suceso H: pacientes de género masculino
a. La probabilidad de que sea de género masculino se refiere a un problema de probabilidad total, ya que es el suceso condicionado y las cirugías los condicionantes. Dicho valor será:
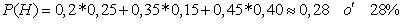
b. Como el suceso condicionado ha ocurrido entonces se aplica el teorema de bayes, luego, el valor de la probabilidad será:
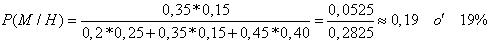
5.-Un Doctor dispone de tres equipos electrónicos para realizar ecosonogramas. El uso que le da a cada equipo es de 25% al primero, 35% el segundo en y 40% el tercero. Se sabe que los aparatos tienen probabilidades de error de 1%, 2% y 3% respectivamente. Un paciente busca el resultado de una ecografía y observa que tiene un error. Determine la probabilidad de que se ha usado el primer aparato.
SOLUCIÓN:
Se definen los sucesos:
Suceso P: seleccionar el primer aparato
Suceso S: seleccionar el segundo aparato
Suceso T: seleccionar el tercer aparato
Suceso E: seleccionar un resultado con error
Se puede observar que la pregunta es sobre determinar la probabilidad de que un examen errado sea del primer aparato, es decir, ya ha ocurrido el error. Por lo tanto, debemos recurrir al teorema de bayes. Claro está, que es necesario de igual forma obtener la probabilidad de que los aparatos produzcan un resultado erróneo, por lo tanto:
6.-Se seleccionan dos semillas aleatoriamente, una por una, de una bolsa que contiene 10 semillas de flores rojas y 5 de flores blancas. ¿Cuál es la probabilidad de que:
- La primera semilla sea roja?
- La segunda semilla sea blanca dado que la primera fue roja?
- La probabilidad de que la primera semilla sea roja es
 ,
puesto que hay 10 semillas de flores rojas de un total de
15. Escrito con notación de probabilidad tenemos:
,
puesto que hay 10 semillas de flores rojas de un total de
15. Escrito con notación de probabilidad tenemos: 
- La probabilidad de que la segunda semilla sea blanca se
ve influida por lo que salió primero, es decir esta
probabilidad está sujeta a una condición, la de que la
primera semilla sea roja. Este tipo de probabilidad se le
llama probabilidad condicional y se denota por

Esta probabilidad
Veamos la situación en un diagrama de árbol:

| Definición
de Probabilidad Condicional: Para
dos eventos cualesquiera A y B en un espacio muestra S,
tales que P(A) > 0 con P(A) ¹ 0, la probabilidad
del evento B dado el evento A, se define por |
Solución: El espacio muestra del experimento de lanzar una moneda 3 veces es
S = {aaa, aas, asa, ass, saa, sas, ssa, sss}
El evento A de que por lo menos hay un águila en los tres lanzamientos es:
A = {aaa, aas, asa, ass, saa, sas, ssa}
El evento B de que obtenga 3 águilas es B = {aaa}
Por lo tanto, AÇ B ={aaa} y
De donde
Nótese que
Proposición 3.5: Para dos eventos A y B cualesquiera del espacio muestra S,
Demostración: Para cualquier evento B,
 |
 |
Despejando P(AÇ B) de la definición de probabilidad condicional, tenemos
P(AÇ B) = P(A) P(B/A) y P(ACÇ B) = P(AC) P (B/AC)
Sustituyendo en [3.3] se tiene P(B) = P(A) P(B/A) + P(AC) P (B/AC).
Obsérvese que en un diagrama de árbol si se multiplica

P(A) P(B/A) = P(AÇ
B) y P(AC) P(B/AC)
= P(ACÇ
B)
8.- Consideremos dos cajas, la caja 1 contiene 3 esferitas blancas y 4 rojas y la caja 2 contiene 8 blancas y 4 rojas. Se selecciona una caja al azar y luego se extrae una esfera al azar. Hallar la probabilidad de que la esfera sea blanca.
Solución: Sea A el evento de seleccionar la caja 1 y AC el evento de seleccionar la caja 2, entonces P(A) = P(AC) = 1/2 ya que cualquiera de las dos cajas tiene la misma probabilidad de ser extraída. Sea B el evento de seleccionar una esfera blanca, entonces P(B/A) = 3/7 ya que en la caja 1 hay 3 esferas blancas en un total de 7 y P(B/AC) = 8/12 porque en la caja 2 hay 8 esferas blancas en un total de 12.
Ahora bien, por la proposición 3.5 tenemos:
9.- Tres máquinas, A, B y C, producen el 45%, 30% y 25%,
respectivamente, del total de las piezas producidas en una
fábrica. Los porcentajes de producción defectuosa de estas máquinas
son del 3%, 4% y 5%.
- Seleccionamos una pieza al azar; calcula la probabilidad de que sea defectuosa.
- Tomamos, al azar, una pieza y resulta ser defectuosa; calcula la probabilidad de haber sido producida por la máquina B.
- ¿Qué máquina tiene la mayor probabilidad de haber producido la citada pieza defectuosa?
Solución:
 Sea D= "la pieza es defectuosa" y N= "la pieza no es defectuosa". La información del problema puede expresarse en el diagrama de árbol adjunto.
Sea D= "la pieza es defectuosa" y N= "la pieza no es defectuosa". La información del problema puede expresarse en el diagrama de árbol adjunto. - Para calcular la probabilidad de que la pieza elegida sea defectuosa, P(D), por la propiedad de la probabilidad total,P(D) = P(A) · P(D/A) + P(B) · P(D/B) + P(C) · P(D/C) =
 = 0.45 · 0.03 + 0.30 · 0.04 + 0.25 · 0.05 = 0.038
= 0.45 · 0.03 + 0.30 · 0.04 + 0.25 · 0.05 = 0.038
- Debemos calcular P(B/D). Por el teorema de Bayes,

- Calculamos P(A/D) y P(C/D), comparándolas con el valor de P(B/D) ya calculado. Aplicando el teorema de Bayes, obtenemos:

La máquina con mayor probabilidad de haber producido la pieza defectuosa es A





12.- Tenemos tres urnas: A con 3 bolas rojas y 5 negras, B con 2 bolas rojas y 1 negra y C con 2 bolas rojas y 3 negras. Escogemos una urna al azar y extraemos una bola. Si la bola ha sido roja, ¿cuál es la probabilidad de haber sido extraída de la urna A?Solución:
 Llamamos R= "sacar bola roja" y N= "sacar bola negra". En el diagrama de árbol adjunto pueden verse las distintas probabilidades de ocurrencia de los sucesos R o N para cada una de las tres urnas.La probabilidad pedida es P(A/R). Utilizando el teorema de Bayes, tenemos:
Llamamos R= "sacar bola roja" y N= "sacar bola negra". En el diagrama de árbol adjunto pueden verse las distintas probabilidades de ocurrencia de los sucesos R o N para cada una de las tres urnas.La probabilidad pedida es P(A/R). Utilizando el teorema de Bayes, tenemos:
No hay comentarios:
Publicar un comentario