1.
DISTRIBUCIÓN BINOMIAL
Las características de esta
distribución son:
a)
En
los experimentos que tienen este tipo de distribución, siempre se esperan dos
tipos de resultados, ejem. Defectuoso, no defectuoso, pasa, no pasa, etc, etc.,
denominados arbitrariamente “éxito” (que es lo que se espera que ocurra) o
“fracaso” (lo contrario del éxito).
b)
Las
probabilidades asociadas a cada uno de estos resultados son constantes, es
decir no cambian.
c)
Cada
uno de los ensayos o repeticiones del experimento son independientes entre sí.
d)
El
número de ensayos o repeticiones del experimento (n) es constante.
A partir de un ejemplo. Desarrollaremos una fórmula que nos
permita cualquier problema que tenga este tipo de distribución.
Ejemplo:
1.-Se lanza al aire una moneda
normal 3 veces, determine la probabilidad de que aparezcan 2 águilas.
Solución:
Antes de empezar a resolver
este problema, lo primero que hay que hacer es identificarlo como un problema que
tiene una distribución binomial, y podemos decir que efectivamente así es, ya
que se trata de un experimento en donde solo se pueden esperar dos tipos de
resultados al lanzar la moneda, águila o sello, cutas probabilidades de
ocurrencia son constantes, cada uno de los lanzamientos es independiente de los
demás y el número de ensayos o repeticiones del experimento son constantes, n =
3.
Para dar solución a este
problema, lo primero que hay que hacer es un diagrama de árbol, en donde
representaremos los tres lanzamientos, de ahí se obtendrá el espacio muestral y
posteriormente la probabilidad pedida, usando la fórmula correspondiente.
A =
águila, S = sello
1/2 S
 A
A S
S
1/2 S
d={AAA, AAS, ASA, ASS,
SAA, SAS, SSA, SSS}
Para obtener la fórmula,
definiremos lo siguiente:
n = número de lanzamientos
de moneda
x = número de “éxitos”
requeridos = número de águilas = 2
p = probabilidad de “éxito”=
p(aparezca águila) =1/2
q = probabilidad de
“fracaso”= p(aparezca sello) =1/2
Entonces podemos partir de
la siguiente expresión para desarrollar la fórmula;
P(aparezcan 2 águilas)=(No.
De ramas del árbol en donde ap. 2 águilas)(probabilidad asociada a cada rama)
Entonces el número de ramas
en donde aparecen dos águilas se puede obtener;
Enumerando las ramas de
interés, estas serían: AAS, ASA, SAA, ¿QUÉ TIPO DE ARREGLOS SON ESTOS ELEMENTOS
DEL ESPACIO MUESTRAL?, Son permutaciones en donde algunos objetos son iguales,
entonces, el número de ramas se puede obtener con la fórmula correspondiente,
donde n = x1+x2+...+xk
sustituyendo en esta
fórmula, tenemos lo siguiente;
esta fórmula puede ser
sustituida por la de combinaciones, solo en el caso de dos tipos de objetos, si
hay más de dos tipos de objetos, definitivamente solo se usa la fórmula
original, como se observará en el caso de la distribución multinomial, pero
¿porqué vamos a cambiar de fórmula?, simplemente porque en todos los libros de
texto que te encuentres vas a encontrar la fórmula de combinaciones en lugar de
la de permutaciones, que es la siguiente,
y sustituyendo valores, nos
damos cuenta de que efectivamente son 3 las ramas de interés, que son donde
aparecen dos águilas, donde n = 3, x = 2.
¿Y la probabilidad asociada
a cada rama?
Probabilidad asociada a cada
rama = p(águila)*p(águila)*p(sello)= p*p*q = p2q=
=
Luego la fórmula de la
distribución Binomial sería:
donde:
p(x, n, p) =
probabilidad de obtener en n ensayos x éxitos, cuando la probabilidad
de éxito es p
Dando
solución al problema de ejemplo tenemos lo siguiente:
n = 3, x = 2, p = ½
Para calcular la media y la
desviación estándar de un experimento que tenga una distribución Binomial usaremos las siguientes fórmulas:
Media o valor esperado.
Donde:
n = número de ensayos o
repeticiones del experimento
P = probabilidad de éxito o
la probabilidad referente al evento del cual se desea calcular la media que se
refiere la media
Q = complemento de P
Desviación estándar.
Ejemplos:
2.-Se dice que el 75% de los accidentes de una planta se
atribuyen a errores humanos. Si en un período de tiempo dado, se suscitan
5 accidentes, determine la probabilidad de que; a) dos de los accidentes
se atribuyan a errores humanos, b) como máximo 1 de los accidentes se
atribuya a errores de tipo humano, c) tres de los accidentes no se atribuyan a errores humanos.
Solución:
a) n = 5
x = variable que nos define
el número de accidentes debidos a errores humanos
x = 0, 1, 2,...,5 accidentes
debidos a errores de tipo humano
p = p(éxito) = p(un
accidente se deba a errores humanos) = 0.75
q = p(fracaso) = p(un
accidente no se deba a errores humanos) = 1-p = 0.25
b) 
c) En este caso cambiaremos
el valor de p;
n =5
x = variable que nos define
el número de accidentes que no se deben a errores de tipo humano
x = 0, 1, 2,...,5 accidentes
debidos a errores humanos
p = p(probabilidad de que un
accidente no se deba a errores humanos) = 0.25
q = p(probabilidad de que un
accidente se deba a errores humanos) = 1-p = 0.75
Solución:
a) n =12
x = variable que nos define
el número de tubos en que el vapor se condensa
x = 0, 1, 2, 3,...,12 tubos
en el que el vapor se condensa
p =p(se condense el vapor en
un tubo de Al a 10 atm)= 0.40
q = p(no se condense el
vapor en un tubo de Al a 10 atm) = 1-p=0.60
= 0.21284
b) p(X=3, 4, ...,12, n=12, p=0.40) =
p(x=3)+p(x=4)+…+p(x=12)= 1-[p(x=0,1,2)]=
= 1-[0.002176+0.0174096+0.06385632]= 1- 0.08344192= 0.91656
c) 
= 0.22703
4.-La probabilidad de que el nivel de ruido de un
amplificador de banda ancha exceda de 2 dB (decibeles) es de 0.15, si se
prueban 10 amplificadores de banda ancha, determine la probabilidad de
que; a) en solo 5 de los amplificadores el nivel de ruido exceda los 2 dB,
b) por lo menos en 2 de los amplificadores, el ruido exceda de 2 dB, c)que
entre 4 y 6 amplificadores no se excedan de los 2 dB, d)encuentre el
número esperado de amplificadores que se exceden de un nivel de ruido de
2dB y su desviación estándar.
Solución:
a)n =10
x =variable que nos define
el número de amplificadores de banda ancha que su nivel de ruido excede de 2 dB
x = 0, 1, 2,...,10 amplificadores
en los que el nivel de ruido excede de los 2 dB
p = P(un amplificador exceda
su nivel de ruido de 2 dB) = 0.15
q = p(un amplificador no
exceda su nivel de ruido de 2 dB =1-p= 0.85
= 0.00849
b)p(x=2,3,...,10,
n=10, p=0.15)= 1- p(x = 0,1) =
= 1 – [(0.19687+(10)(0.15)(0.231617)]=1-0.544296 = 0.455705
c) n=10
x= variable que nos define
el número de amplificadores de banda ancha que su nivel de ruido no excede de 2
dB
x= 0, 1, 2,...,10
amplificadores que su nivel de ruido no excede de los 2 dB
p = p(un amplificador no
exceda su nivel de ruido de 2 dB) = 0.85
q = p(un amplificador exceda
su nivel de ruido de 2 dB) = 1- p = 0.15
=(210)(0.522)(0.00001139)+(252)(0.4437)(0.000075937)+(210)(0.3771495)(0.00005063)=
=0.001249 +
0.00849 + 0.00400997 = 0.01374897
d)n=10, p=0.15, q=1-p=0.85
Interpretación:
Se espera que 2 de los 10
amplificadores probados se excedan de un nivel de ruido de 2 Db
Interpretación:
Este
experimento puede variar en 2 ± 1 amplificador, esto es, de
1 a 3 amplificadores que se excedan de un nivel de ruido de 2 dB
5.-La última novela de un autor ha tenido un gran
éxito, hasta el punto de que el 80% de los lectores ya la han leido. Un
grupo de 4 amigos son aficionados a la lectura:
1. ¿Cuál es la probabilidad de que el grupo hayan leido la novela 2 personas?
n = 4
p = 0.8
q = 0.2
B(4, 0.8)

2.¿Y al menos 2?

Parámetros de la distribución binomial
Media
Varianza
Desviación típica
Ejemplo
6.-La probabilidad de que un artículo
producido por una fabrica sea defectuoso es 0.02. Se envió un cargamento
de 10.000 artículos a unos almacenes. Hallar el número esperado de
artículos defectuosos, la varianza y la desviación típica.

Ejercicio 8

Ejercicio 9

Ejercicio 10

11.-"Un examen tipo test consta de 10 preguntas, cada una de ellas con tres posibles respuestas, de forma que sólo una de las tres es correcta. ¿Cuál es la probabilidad de que un estudiante que contesta al azar acierte 6?"
Definimos X="Número de aciertos en las 10 preguntas". En este caso, cada pregunta es cada una de las pruebas que se repiten, o sea, n = 10.
De la manera que está planteado el problema sólo hay dos posibles resultados, o acierta (éxito, pues me preguntan sobre los aciertos) o no acierta (fracaso) y la probabilidad de acierto en cada prueba es la misma, 1 / 3.
Por tanto efectivamente X sigue una distribución binomial ; X es B(10, 1/3) y el problema me pide P [ X = 6 ]
Para calcular esa probabilidad, observamos que X = 6 significa 6 aciertos y 4 fallos, o sea (1 / 3 ) 6 · (2 / 3 ) 4. Además hay que tener en cuenta cómo repartir los 6 acierto a lo largo de las 10 preguntas; no importa el orden y no se pueden repetir las preguntas, por tanto combinación sin repetición de 10 elementos tomados de 6 en 6.Luego la probabilidad pedida es:
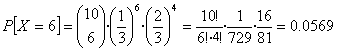
12. Un agente de seguros vende pólizas a cinco personas de la misma edad y que disfrutan de buena salud. Según las tablas actuales, la probabilidad de que una persona en esta s condiciones viva 30 años o más es 2/3. Hállese la probabilidad de que, transcurridos 30 años, vivan:
13Las cinco personas.
B(5, 2/3) p = 2/3 q = 1/3

14.Al menos tres personas.

15.Exactamente dos personas.

16.-Si de seis a siete de la tarde se admite que un número de teléfono de cada cinc
o está comunicando, ¿cuál es la probabilidad de que, cuando se marquen
10 números de teléfono elegidos al azar, sólo comuniquen dos?
o está comunicando, ¿cuál es la probabilidad de que, cuando se marquen
10 números de teléfono elegidos al azar, sólo comuniquen dos?
B(10, 1/5)p = 1/5q = 4/5

17.-La probabilidad de que un hombre acierte en el blanco es 1/4. Si dispara 10 veces
¿cuál es la probabilidad de que acierte exactamente en tres ocasiones?
¿Cuál es la probabilidad de que acierte por lo menos en una ocasión?
¿cuál es la probabilidad de que acierte exactamente en tres ocasiones?
¿Cuál es la probabilidad de que acierte por lo menos en una ocasión?
B(10, 1/4) p = 1/4q = 3/4


En una urna hay 30 bolas, 10 rojas y el resto blancas. Se elige una bola al azar
y se anota si es roja; el proceso se repite, devolviendo la bola, 10 veces.
Calcular la media y la desviación típica.
B(10, 1/3) p = 1/3q = 2/3
18.-lanza una moneda cuatro veces. Calcular la probabilidad de que salgan más
caras que cruces
.
caras que cruces
.
B(4, 0.5) p = 0.5q = 0.5

No hay comentarios:
Publicar un comentario