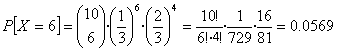Esperanza matemática

La esperanza matemática o valor esperado de una variable aleatoria discreta es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso.

Los nombre de esperanza matemática y valor esperado tienen su origen en los juegos de azar y hacen referencia a la ganancia promedio esperada por un jugador cuando hace un gran número de apuestas.

Si la esperanza matemática es cero, E(x) = 0, el juego es equitativo, es decir, no existe ventaja ni para el jugador ni para la banca.

Ejemplos

1.- Si una persona compra una papeleta en una rifa, en la que puede ganar de 5.000 € ó un segundo premio de 2000 € con probabilidades de: 0.001 y 0.003. ¿Cuál sería el precio justo a pagar por la papeleta?

E(x) = 5000 · 0.001 + 2000 · 0.003 = 11 €

2.- Un jugador lanza dos monedas. Gana 1 ó 2 € si aparecen una o dos caras. Por otra parte pierde 5 € si no aparece cara. Determinar la esperanza matemática del juego y si éste es favorable.

E = {(c,c);(c,x);(x,c);(x,x)}

p(+1) = 2/4

p(+2) = 1/4

p(−5) = 1/4

E(x)= 1 · 2/4 + 2 · 1/4 - 5 · 1/4 = −1/4. Es desfavorable

3.- En una ciudad, la temperatura máxima durante el mes de junio está distribuida normalmente con una media de 26º y una desviación típica de 4º.
Calcular el número de días que se "espera", tengan temperatura máxima comprendida entre 22º y 28º.

Como se trata de una distribución Normal, tipificamos (estandarizamos) los valores 22 y 28:
z1= (22 – 26) / 4 = -1
z2 = (28 – 26) / 4 = 0, 5
Entonces la probabilidad de que en un día de junio la temperatura máxima esté entre 22 y 28º es:
p( 22< x < 28) = p( -1 < z < 0,5 ) = 0, 5328
Y el número esperado (esperanza) de días es:
E(x) = n * p = 30 * 0, 5328 ≈ 16 días

4.-

Ejemplo. Si X es el número de puntos obtenidos al lanzar un dado de seis caras, encontremos el valor esperado de la variable aleatoria Y = X² .

La función de probabilidad de X es f(x) = 1/6 si xÎ{1,2,3,4,5,6}. La función de probabilidad

de Y = X² es entonces f(y) = 1/6 si yÎ{1,4,9,16,25,36}, así E(Y) = 1/6*1 + 1/6*4 + 1/6*9 + 1/6*16 + 1/6*25 + 1/6*36 = 1²*P(X=1) + 2²*P(X= 2) + 3²*P(X= 3) + 4²*P(X= 4) + 5²*P(X= 5) + 6²*P(X= 6) = å X²*P(X=x)

Ejemplo. Supongamos ahora que X es una v.a. que tiene función de probabilidad f(x) = 1/6 si xÎ{-2,-1,0,1,2,3}y Y = X² . La función de probabilidad de Y es f(y) = 2/6 si yÎ{1, 4} y f(y) = 1/6 si yÎ{0, 9}. Entonces E(Y) = 2/6*1 + 2/6*4 + 1/6*0 + 1/6*9. Esta ecuación puede escribirse de la siguiente manera: E(Y) = 2/6*1 + 2/6*4 + 1/6*0 + 1/6*9 = 1*P(Y=1) + 4*P(Y=4) + 0*P(Y=0) + 9*P(Y=1) = 1²*P(X=1 ó X=-1) + 2²*P(X=2 ó X=-2) + 0²*P(X=0) + 3²*P(X=3) = å X²*P(X=x)

A través de estos ejemplos vemos que no es necesario calcular la función de probabilidad de Y, sólo tenemos que usar la función de probabilidad de X y los valores obtenidos al aplicar la

función Y = g(X) = X² . Esto es cierto aún en el caso en que la función no es uno-uno.

LA VARIANZA

La varianza la denotamos mediante V(X) o VAR(X) o s², y se calcula como,

Obsérvese que del mismo modo en que se demuestra la relación se comprueba que

V(X)=E(X²)-(E(X))²

Similarmente, V(a+bX)=b^2.V(X)=b²s²

Ejemplo. Consideramos una variable aleatoria discreta con función de probabilidad,

Obtener el valor de la constante c para que sea una función de probabilidad, los valores de las funciones de probabilidad y distribución para todos los valores de x, y P(x=3), y P(x≤3).

Solución: Para ello consideramos,

ya que tenemos la suma de una progresión geométrica de razón menor que la unidad:

Calculemos sucesivos valores de f(x) y F(x),

x	2	3	4	5	…
f(x)	3/4	3/16	3/64	3/256	…
F(x)	0.75	0.94	0.987	0.999	….

Y como se observa que: si x crece, f(x) decrece y F(x) crece hasta llegar a su máximo valor 1

P(X=3)=f(3)=0.047 P(X≤3)=0.987

Ejemplo para la variable aleatoria continua, función de densidad

Hallar: El valor de la constante c para que sea una función de densidad, la función de distribución, el valor medio, y la probabilidad de que la variable este comprendida entre 0,2 y 0,7

Solución. Consideremos,

La cual debe ser de valor 1, entonces c/4=1, esto es, c=4

luego, la función de distinción acumulada es F(x)=x⁴para 0<x≤1, 0 en valores x≤0 y 1 para x≥1

El valor medio es

P(0.2≤x≤0.7)=F(0.7)-F(0.2)=0.7²-0.2²=0.24

Ejemplo, Calcule la varianza de la variable aleatoria x, que representa el número de puntos obtenidos con un dado.

m=E(X)=1*1/6+2*1/6+3*1/6+4*1/6+5*1/6+6*1/6

m^`₂=E(X²)=1²*1/6+2²*1/6+3²*1/6+4²*1/6+5²*1/6+6²*1/6

Sabemos que s2=m`₂-m²=((91/6)-(7/2)²=35/12

10.-n pediatra obtuvo la siguiente tabla sobre los meses de edad de 50 niños de su consulta en el momento de andar por primera vez:

Meses	Niños
9	1
10	4
11	9
12	16
13	11
14	8
15	1

11.-Calcular la varianza.

x_i	f_i	N_i	x_i · f_i	x²_i · f_i
9	1	1	9	81
10	4	5	40	400
11	9	14	99	1089
12	16	30	192	2304
13	11	41	143	1859
14	8	49	112	1568
15	1	50	15	225
	50		610	7526

12.-Media aritmética

13.-Varianza

3.El resultado de lanzar dos dados 120 veces viene dado por la tabla:

Sumas	2	3	4	5	6	7	8	9	10	11	12
Veces	3	8	9	11	20	19	16	13	11	6	4

14.- Calcular desviación típica.

x_i	f_i	x_i · f_i	x_i² · f_i
2	3	6	12
3	8	24	72
4	9	36	144
5	11	55	275
6	20	120	720
7	19	133	931
8	16	128	1024
9	13	117	1053
10	11	110	1100
11	6	66	726
12	4	48	576
	120	843	6633

15.-Calcular la varianza de una distribución estadística que viene dada por la siguiente tabla:

	[10, 15)	[15, 20)	[20, 25)	[25, 30)	[30, 35)
f_i	3	5	7	4	2

	x_i	f_i	x_i · f_i	x_i² · f_i
[10, 15)	12.5	3	37.5	468.75
[15, 20)	17.5	5	87.5	1537.3
[20, 25)	22.5	7	157.5	3543.8
[25, 30)	27.5	4	110	3025
[30, 35)	32.5	2	65	2112.5
		21	457.5	10681.25

16.-Media

17.-Varianza

18.-Calcular la varianza de la distribución de la tabla:

	x_i	f_i	x_i · f_i	x_i² · f_i
[10, 20)	15	1	15	225
[20, 30)	25	8	200	5000
[30,40)	35	10	350	12 250
[40, 50)	45	9	405	18 225
[50, 60	55	8	440	24 200
[60,70)	65	4	260	16 900
[70, 80)	75	2	150	11 250
		42	1 820	88 050

19.-Las alturas de los jugadores de un equipo de baloncesto vienen dadas por la tabla:

Altura	[170, 175)	[175, 180)	[180, 185)	[185, 190)	[190, 195)	[195, 2.00)
Nº de jugadores	1	3	4	8	5	2

Calcula la varianza.

	x_i	f_i	F_i	x_i · f_i	x_i² · f_i
[1.70, 1.75)	1.725	1	1	1.725	2.976
[1.75, 1.80)	1.775	3	4	5.325	9.453
[1.80, 1.85)	1.825	4	8	7.3	13.324
[1.85, 1.90)	1.875	8	16	15	28.128
[1.90, 1.95)	1.925	5	21	9.625	18.53
[1.95, 2.00)	1.975	2	23	3.95	7.802
		23		42.925	80.213

20.-Media

Varianza

7.Dada la distribución estadística:

	[0, 5)	[5, 10)	[10, 15)	[15, 20)	[20, 25)	[25, ∞)
f_i	3	5	7	8	2	6

Calcular la varianza.

	x_i	f_i	F_i
[0, 5)	2.5	3	3
[5, 10)	7.5	5	8
[10, 15)	12.5	7	15
[15, 20)	17.5	8	23
[20, 25)	22.5	2	25
[25, ∞)		6	31
		31

Media

No se puede calcular la media, porque no se puede hallar la marca de clase del último intervalo.

Varianza

Si no hay media no es posible hallar la varianza.

8.Considérense los siguientes datos: 3, 8, 4, 10, 6, 2. Se pide:

1. Calcular su media y su varianza.

2. Si los todos los datos anteriores los multiplicamos por 3, cúal será la nueva media y varianza.

x_i	x_i²
2	4
3	9
4	16
6	36
8	64
10	100
33	229

1

2

1. DISTRIBUCIÓN BINOMIAL

Las características de esta distribución son:

a) En los experimentos que tienen este tipo de distribución, siempre se esperan dos tipos de resultados, ejem. Defectuoso, no defectuoso, pasa, no pasa, etc, etc., denominados arbitrariamente “éxito” (que es lo que se espera que ocurra) o “fracaso” (lo contrario del éxito).

b) Las probabilidades asociadas a cada uno de estos resultados son constantes, es decir no cambian.

c) Cada uno de los ensayos o repeticiones del experimento son independientes entre sí.

d) El número de ensayos o repeticiones del experimento (n) es constante.

A partir de un ejemplo. Desarrollaremos una fórmula que nos permita cualquier problema que tenga este tipo de distribución.

Ejemplo:

1.-Se lanza al aire una moneda normal 3 veces, determine la probabilidad de que aparezcan 2 águilas.

Solución:

Antes de empezar a resolver este problema, lo primero que hay que hacer es identificarlo como un problema que tiene una distribución binomial, y podemos decir que efectivamente así es, ya que se trata de un experimento en donde solo se pueden esperar dos tipos de resultados al lanzar la moneda, águila o sello, cutas probabilidades de ocurrencia son constantes, cada uno de los lanzamientos es independiente de los demás y el número de ensayos o repeticiones del experimento son constantes, n = 3.

Para dar solución a este problema, lo primero que hay que hacer es un diagrama de árbol, en donde representaremos los tres lanzamientos, de ahí se obtendrá el espacio muestral y posteriormente la probabilidad pedida, usando la fórmula correspondiente.

A = águila, S = sello

1/2 A

1/2 S

1/2 A

1/2 1/2 S

1/2 A

1/2 1/2 S

1/2 A

1/2 S

d={AAA, AAS, ASA, ASS, SAA, SAS, SSA, SSS}

Para obtener la fórmula, definiremos lo siguiente:

n = número de lanzamientos de moneda

x = número de “éxitos” requeridos = número de águilas = 2

p = probabilidad de “éxito”= p(aparezca águila) =1/2

q = probabilidad de “fracaso”= p(aparezca sello) =1/2

Entonces podemos partir de la siguiente expresión para desarrollar la fórmula;

P(aparezcan 2 águilas)=(No. De ramas del árbol en donde ap. 2 águilas)(probabilidad asociada a cada rama)

Entonces el número de ramas en donde aparecen dos águilas se puede obtener;

Enumerando las ramas de interés, estas serían: AAS, ASA, SAA, ¿QUÉ TIPO DE ARREGLOS SON ESTOS ELEMENTOS DEL ESPACIO MUESTRAL?, Son permutaciones en donde algunos objetos son iguales, entonces, el número de ramas se puede obtener con la fórmula correspondiente,

donde n = x₁+x₂+...+x_k

sustituyendo en esta fórmula, tenemos lo siguiente;

esta fórmula puede ser sustituida por la de combinaciones, solo en el caso de dos tipos de objetos, si hay más de dos tipos de objetos, definitivamente solo se usa la fórmula original, como se observará en el caso de la distribución multinomial, pero ¿porqué vamos a cambiar de fórmula?, simplemente porque en todos los libros de texto que te encuentres vas a encontrar la fórmula de combinaciones en lugar de la de permutaciones, que es la siguiente,

y sustituyendo valores, nos damos cuenta de que efectivamente son 3 las ramas de interés, que son donde aparecen dos águilas, donde n = 3, x = 2.

¿Y la probabilidad asociada a cada rama?

Probabilidad asociada a cada rama = p(águila)*p(águila)*p(sello)= p*p*q = p²q=

Luego la fórmula de la distribución Binomial sería:

donde:

p(x, n, p) = probabilidad de obtener en n ensayos x éxitos, cuando la probabilidad de éxito es p

Dando solución al problema de ejemplo tenemos lo siguiente:

n = 3, x = 2, p = ½

Para calcular la media y la desviación estándar de un experimento que tenga una distribución Binomial usaremos las siguientes fórmulas:

Media o valor esperado.

Donde:

n = número de ensayos o repeticiones del experimento

P = probabilidad de éxito o la probabilidad referente al evento del cual se desea calcular la media que se refiere la media

Q = complemento de P

Desviación estándar.

Ejemplos:

2.-Se dice que el 75% de los accidentes de una planta se atribuyen a errores humanos. Si en un período de tiempo dado, se suscitan 5 accidentes, determine la probabilidad de que; a) dos de los accidentes se atribuyan a errores humanos, b) como máximo 1 de los accidentes se atribuya a errores de tipo humano, c) tres de los accidentes no se atribuyan a errores humanos.

Solución:

a) n = 5

x = variable que nos define el número de accidentes debidos a errores humanos

x = 0, 1, 2,...,5 accidentes debidos a errores de tipo humano

p = p(éxito) = p(un accidente se deba a errores humanos) = 0.75

q = p(fracaso) = p(un accidente no se deba a errores humanos) = 1-p = 0.25

c) En este caso cambiaremos el valor de p;

n =5

x = variable que nos define el número de accidentes que no se deben a errores de tipo humano

x = 0, 1, 2,...,5 accidentes debidos a errores humanos

p = p(probabilidad de que un accidente no se deba a errores humanos) = 0.25

q = p(probabilidad de que un accidente se deba a errores humanos) = 1-p = 0.75

3.-Si la probabilidad de que el vapor se condense en un tubo de aluminio de cubierta delgada a 10 atm de presión es de 0.40, si se prueban 12 tubos de ese tipo y bajo esas condiciones, determine la probabilidad de que: a) el vapor se condense en 4 de los tubos, b) en más de 2 tubos se condense el vapor, c) el vapor se condense en exactamente 5 tubos.

Solución:

a) n =12

x = variable que nos define el número de tubos en que el vapor se condensa

x = 0, 1, 2, 3,...,12 tubos en el que el vapor se condensa

p =p(se condense el vapor en un tubo de Al a 10 atm)= 0.40

q = p(no se condense el vapor en un tubo de Al a 10 atm) = 1-p=0.60

= 0.21284

b) p(X=3, 4, ...,12, n=12, p=0.40) = p(x=3)+p(x=4)+…+p(x=12)= 1-[p(x=0,1,2)]=

= 1-[0.002176+0.0174096+0.06385632]= 1- 0.08344192= 0.91656

= 0.22703

4.-La probabilidad de que el nivel de ruido de un amplificador de banda ancha exceda de 2 dB (decibeles) es de 0.15, si se prueban 10 amplificadores de banda ancha, determine la probabilidad de que; a) en solo 5 de los amplificadores el nivel de ruido exceda los 2 dB, b) por lo menos en 2 de los amplificadores, el ruido exceda de 2 dB, c)que entre 4 y 6 amplificadores no se excedan de los 2 dB, d)encuentre el número esperado de amplificadores que se exceden de un nivel de ruido de 2dB y su desviación estándar.

Solución:

a)n =10

x =variable que nos define el número de amplificadores de banda ancha que su nivel de ruido excede de 2 dB

x = 0, 1, 2,...,10 amplificadores en los que el nivel de ruido excede de los 2 dB

p = P(un amplificador exceda su nivel de ruido de 2 dB) = 0.15

q = p(un amplificador no exceda su nivel de ruido de 2 dB =1-p= 0.85

= 0.00849

b)p(x=2,3,...,10, n=10, p=0.15)= 1- p(x = 0,1) =

= 1 – [(0.19687+(10)(0.15)(0.231617)]=1-0.544296 = 0.455705

c) n=10

x= variable que nos define el número de amplificadores de banda ancha que su nivel de ruido no excede de 2 dB

x= 0, 1, 2,...,10 amplificadores que su nivel de ruido no excede de los 2 dB

p = p(un amplificador no exceda su nivel de ruido de 2 dB) = 0.85

q = p(un amplificador exceda su nivel de ruido de 2 dB) = 1- p = 0.15

=(210)(0.522)(0.00001139)+(252)(0.4437)(0.000075937)+(210)(0.3771495)(0.00005063)=

=0.001249 + 0.00849 + 0.00400997 = 0.01374897

d)n=10, p=0.15, q=1-p=0.85

Interpretación:

Se espera que 2 de los 10 amplificadores probados se excedan de un nivel de ruido de 2 Db

Interpretación:

Este experimento puede variar en 2 ± 1 amplificador, esto es, de 1 a 3 amplificadores que se excedan de un nivel de ruido de 2 dB

5.-La última novela de un autor ha tenido un gran éxito, hasta el punto de que el 80% de los lectores ya la han leido. Un grupo de 4 amigos son aficionados a la lectura:

1. ¿Cuál es la probabilidad de que el grupo hayan leido la novela 2 personas?

n = 4

p = 0.8

q = 0.2

B(4, 0.8)

2.¿Y al menos 2?

Parámetros de la distribución binomial

Media

Varianza

Desviación típica

Ejemplo

6.-La probabilidad de que un artículo producido por una fabrica sea defectuoso es 0.02. Se envió un cargamento de 10.000 artículos a unos almacenes. Hallar el número esperado de artículos defectuosos, la varianza y la desviación típica.

Ejercicio 7

Problemas resueltos distribución binomial.

Ejercicio 8

Problemas resueltos distribución binomial.

Ejercicio 9

Problemas resueltos distribución binomial.

Ejercicio 10

Problemas distribución binomial.

11.-"Un examen tipo test consta de 10 preguntas, cada una de ellas con tres posibles respuestas, de forma que sólo una de las tres es correcta. ¿Cuál es la probabilidad de que un estudiante que contesta al azar acierte 6?"

Definimos X="Número de aciertos en las 10 preguntas". En este caso, cada pregunta es cada una de las pruebas que se repiten, o sea, n = 10.
De la manera que está planteado el problema sólo hay dos posibles resultados, o acierta (éxito, pues me preguntan sobre los aciertos) o no acierta (fracaso) y la probabilidad de acierto en cada prueba es la misma, 1 / 3.

Por tanto efectivamente X sigue una distribución binomial ; X es B(10, 1/3) y el problema me pide P [ X = 6 ]

Para calcular esa probabilidad, observamos que X = 6 significa 6 aciertos y 4 fallos, o sea (1 / 3 ) ⁶ · (2 / 3 ) ⁴. Además hay que tener en cuenta cómo repartir los 6 acierto a lo largo de las 10 preguntas; no importa el orden y no se pueden repetir las preguntas, por tanto combinación sin repetición de 10 elementos tomados de 6 en 6.Luego la probabilidad pedida es:

12. Un agente de seguros vende pólizas a cinco personas de la misma edad y que disfrutan de buena salud. Según las tablas actuales, la probabilidad de que una persona en esta s condiciones viva 30 años o más es 2/3. Hállese la probabilidad de que, transcurridos 30 años, vivan:

13Las cinco personas.

B(5, 2/3) p = 2/3 q = 1/3

14.Al menos tres personas.

15.Exactamente dos personas.

16.-Si de seis a siete de la tarde se admite que un número de teléfono de cada cinc
o está comunicando, ¿cuál es la probabilidad de que, cuando se marquen
10 números de teléfono elegidos al azar, sólo comuniquen dos?

B(10, 1/5)p = 1/5q = 4/5

17.-La probabilidad de que un hombre acierte en el blanco es 1/4. Si dispara 10 veces
¿cuál es la probabilidad de que acierte exactamente en tres ocasiones?
¿Cuál es la probabilidad de que acierte por lo menos en una ocasión?

B(10, 1/4) p = 1/4q = 3/4