1. En una clase de 35 alumnos se quiere elegir un comité formado por tres alumnos. ¿Cuántos comités diferentes se pueden formar?
No entran todos los elementos.
No importa el orden: Juan, Ana.
No se repiten los elementos.
2. ¿De cuántas formas pueden mezclarse los siete colores del arco iris tomándolos de tres en tres?
No entran todos los elementos.
No importa el orden.
No se repiten los elementos.

3. A una reunión asisten 10 personas y se intercambian saludos entre todos. ¿Cuántos saludos se han intercambiado?
No entran todos los elementos.
No importa el orden.
No se repiten los elementos.
4. En una bodega hay en un cinco tipos diferentes de botellas. ¿De cuántas formas se pueden elegir cuatro botellas?
No entran todos los elementos. Sólo elije 4..
No importa el orden. Da igual que elija 2 botellas de anís y 2 de ron, que 2 de ron y 2 de anís.
Sí se repiten los elementos. Puede elegir más de una botella del mismo tipo.

5. ¿Cuántas
apuestas de Lotería Primitiva de una columna han de rellenarse para
asegurarse el acierto de los seis resultados, de 49?
No entran todos los elementos.
No importa el orden.
No se repiten los elementos.
6. ¿Cuántas diagonales tiene un pentágono y cuántos triángulos se puede informar con sus vértices?
Vamos a determinar en primer lugar las rectas que se pueden trazar entre 2 vértices.
No entran todos los elementos.
No importa el orden.
No se repiten los elementos.
Son  , a las que tenemos que restar los lados que determinan 5 rectas que no son diagonales.
, a las que tenemos que restar los lados que determinan 5 rectas que no son diagonales.
7. Un
grupo, compuesto por cinco hombres y siete mujeres, forma un comité de 5
hombres y 3 mujeres. De cuántas formas puede formarse, si:
1. Puede pertenecer a él cualquier hombre o mujer.
2. Una mujer determinada debe pertenecer al comité.
3. Dos hombres determinados no pueden estar en el comité.
8. Una persona tiene cinco monedas de distintos valores. ¿Cuántas sumas diferentes de dinero puede formar con las cinco monedas?
9.Con las cifras 1, 2, 3, 4, 5, 6 y 7 ¿cuántos
productos diferentes puedo conseguir si las tomo de 2 en dos y cuáles
son los factores?
Respuesta: 21 productos y son: 

Nota.- Cada grupo debe tener un elemento
distinto para que los productos sean diferentes. El orden de los
factores no cambia el resultado del producto.
10. ¿De cuántas formas puedo agrupar los números 1, 2, 3, 4 y 5 constando cada uno por 3 elementos?
Se desea ver cada número formado.
Se desea ver cada número formado.
Respuesta: 35 números que son:
111 112 113 114 115 122 123 124 125 133 134 135 144
145 155 222 223 224 225 233 234 235 244 245 255 333
334 335 344 345 355 444 445 455 555
11. ¿Cuántas combinaciones puedes hacer con las cifras 1, 2, 3, 4, y 5 tomadas de 3 en 3 de modo que el número 3 se halle en todos los grupos?
Respuesta: 6111 112 113 114 115 122 123 124 125 133 134 135 144
145 155 222 223 224 225 233 234 235 244 245 255 333
334 335 344 345 355 444 445 455 555
11. ¿Cuántas combinaciones puedes hacer con las cifras 1, 2, 3, 4, y 5 tomadas de 3 en 3 de modo que el número 3 se halle en todos los grupos?
Solución
Con las cinco cifras puedes hacer 10 números diferentes de 3 cifras cada uno:

De las 30 cifras, 6 corresponderán al 1, 6 al 2, 6 al 3, etc., y esto quiere decir, que habrá:  números que contienen a cada una de ellas: 123 124 125 134 135 145 234 235 245 345
números que contienen a cada una de ellas: 123 124 125 134 135 145 234 235 245 345
Podrás comprobar 6 números contienen el 1
6 números contienen el 2
6 números contienen el 3
6 números contienen el 4
6 números contienen el 5
 números que contienen a cada una de ellas: 123 124 125 134 135 145 234 235 245 345
números que contienen a cada una de ellas: 123 124 125 134 135 145 234 235 245 345Podrás comprobar 6 números contienen el 1
6 números contienen el 2
6 números contienen el 3
6 números contienen el 4
6 números contienen el 5
12. ¿De cuántas maneras se pueden sentar 10 personas alrededor de una mesa?
Respuesta:
13. ¿Cuántas quinielas de fútbol tengo que rellenar para sacar una de 14?
Respuesta:
Solución
En cada partido, un equipo puede: ganar, empatar o perder y esto se repite en 14 partidos, luego tendremos:
En cada partido, un equipo puede: ganar, empatar o perder y esto se repite en 14 partidos, luego tendremos:
14. Un hospital cuenta con 21 cirujanos con los cuales hay que formar ternas para
realizar guardias. ¿Cuántas ternas se podrán formar?
Se trata de formar todas las ternas posibles, sin repetir elementos en cada una, y sin
importar el orden de los elementos.Si quisiéramos formar todas las ternas posibles, sin repetición de elementos en cada una, para elegir el primer elemento hay 21 posibilidades, para el segundo quedan 20 posibilidades, y para el tercero 19 posibilidades, por lo tanto el número de ternas posibles está dado por: 21* 20*19 = 7980
Pero en este caso cada terna aparece repetida en distinto orden, por ejemplo tendremos: ABC, ACB, BAC, CAB y CBA. Son seis ternas con los mismos elementos, que está dado por el factorial de 3.
Por lo tanto el total de ternas obtenido 7980, hay que dividirlo por 6
7980/6 = 1330
15.-En una bodega hay en un cinco tipos diferentes de botellas. ¿De cuántas formas se pueden elegir cuatro botellas?
No entran todos los elementos. Sólo elije 4..
No importa el orden. Da igual que elija 2 botellas de anís y 2 de ron, que 2 de ron y 2 de anís.
Sí se repiten los elementos. Puede elegir más de una botella del mismo tipo.
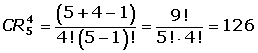
16. ¿Cuántas fichas tiene el juego del dominó?
Una ficha de dominó es un rectángulo en el que hay dos partes, en cada una de ellas hay una serie de puntos que indican la puntuación de esa parte. Estas puntuaciones van de blanca (0 puntos) a 6. Tenemos pares de puntuaciones de 0 a 6.
El total de fichas será
Nota: Si nos gusta un pastel lo podemos pedir hasta cuatro veces.
Estamos en el caso en el que no nos importa el orden en que elijamos los pasteles y podemos repetir, son combinaciones con repetición.
como no hay orden son combinaciones)
C de 7 en 3= 7 * 6* 5 / 3 * 2 *1 = 210 / 6 = 35 equipos
19.Un examen consta de 10 preguntas de las cuales solo se pueden elegir 8, de cuantas maneras se puede resolver el examen: (como no hay orden son combinaciones)
C de 10 en 8= 10*9*8*7*6*5*4*3 / 8*7*6*5*4*3*2*1 = 1814400/ 40320 = 45 maneras
20. Si se seleccionan cinco cartas de un grupo de nueve, ¿cuantas combinaciones de cinco cartas habría?
La cantidad de combinaciones posibles sería: P(9,5)/5! = (9*8*7*6*5)/(5*4*3*2*1) = 126 combinaciones posibles.
bacano
ResponderEliminarGracias me ayudo de mucho
ResponderEliminarMi problema es el siguiente: hay 10 empresas distintas entre si, que serán inspeccionadas cada una por un grupo de 4 personas, a cada una de ellas va un grupo un día jueves de la semana.
ResponderEliminarPero cada jueves estos grupos de cuarenta personas se deben cambiar entre ellas y volver a formar 10 grupos de cuatro personas e ir a una empresa diferente, sin que suceda que una persona se repita la empresa a la que fue anteriormente.
Complica esto que cada vez que hay inspección, en cada grupo una persona hace de lidere y otra hace el informe que resultó de la inspección.
Por lo tanto, en el rotar de cada jueves, ninguno puede ser lidere o hacedor del informe tres veces seguidas.
Esto tiene solución? Existe un programa que lo realice metiendo los datos? o una forma simple de hacer la rotación, con los restricciones indicadas?
mi correo es:
ResponderEliminarnnolivares@gmail.com
Gracias.
Mi problema es:
ResponderEliminarSe van a hacer 2 pasteles con 8 sabores diferentes ¿ cuantas combinaciones posibles hay?
Combinación sin repetición..
EliminarEs una combinación simple
X la tanto la respuesta: es 28
Muy bien...
ResponderEliminarMuy bien...
ResponderEliminarayuda porfa
ResponderEliminar4. ) De un grupo de 7 administradores y 10 de comercio internacional se quiere formar un comité de 5 personas para investigación. ¿Cuántos comités de 5 personas es posible formar si en cada comité debe haber máximo 3 administradores?.
el profe leonel se enterara de esto
Eliminar3. Lina tiene cuatro fichas, cada una con una letra de la palabra ROMA responde:
ResponderEliminara. ¿Cuántas palabras diferentes sin importar su resultado puede formar con dichas letras?
b. ¿Cuáles de esas palabras tienen algún resultado en el idioma español?
c. Si las palabras solo pueden empezar con una vocal ¿Cuántas palabras se podrían formar?
d. Si las palabras solo pueden comenzar con una consonante ¿cuántas palabras se podrían formar?
4 factorial sobre o factorial =24
Eliminarbuen dia mi problema es el siguiente si alguien me puede ayudar gracias:
ResponderEliminarcuantas posibles combinaciones tiene un candado de clave que tiene tambores con dígitos cada uno y una letra?
buen dia mi problema es el siguiente si alguien me puede ayudar gracias:
ResponderEliminarcuantas posibles combinaciones tiene un candado de clave que tiene cinco tambores con 10 dígitos cada uno y una letra?
Al final del día, una pastelería dona todo lo que no pudo vender a centros de ayuda para los necesitados. Si al final de un día dado, le quedan 20 pasteles de manzana, ¿de Cuantas maneras diferentes puede repartir estos pasteles entre 8 centros de acopio?la caja, uno después del otro sin reemplazo
ResponderEliminarDe la siguiente lista se eligen 6 números: -7,-6-5, -4, -3, -2, -1, 1, 2, 3, 4,5,6,7 . ¿De cuántas formas se puede hacer la selección de modo que el producto de los cuatro números sea negativo y los números sean distintos?
ResponderEliminar¿Cuantos comités diferentes de 3 Hombres y 6 Mujeres pueden formarse a partir de un grupo formado por 20 Hombres y 15 Mujeres?
ResponderEliminarSe tiene una urna con 20 bolas numeradas. Se quiere saber, ¿de cuántas maneras podemos sacar primero 3 bolas, luego 4 y finalmente 5?
ResponderEliminar4 chicas y tres varones van al cine y encuentran asientos juntos en una misma fila, donde desean acomodarse.¿De cuántas maneras diferentes pueden sentarse si las dos de las sietes chicas no quieren estar juntas?
ResponderEliminarSe tienen bolitas marcadas con los dígitos :1, 2, 3, 4, 5 .¿Cuántos números se pueden obtener?
ResponderEliminarPoruqe el de divide para 6 en al los cirujanos
ResponderEliminarHalle el numero de 10 conbinaciones tomando de 4 en 4
ResponderEliminarY si en vez de encontrar coMbinaciones... aprendieran un poco el castellano?????
ResponderEliminarde cuantas formas se puede escoger tres fenotipos de un grupo de 20 si a:
ResponderEliminara.-hay reemplazo y b.-no hay reemplazo
porfavor me podrias contestar a mi pregunta
EliminarNo entiendo porqué en el ejercicio 4 lo clasifica como una combinación con repetición, si desde el enunciado no se establece que lo haya; y si es así sería contradictorio con el punto 1 si el planteamiento es el mismo.
ResponderEliminarhola mi problema es este:
ResponderEliminarEl comité de seguridad de la fábrica de zapatos debe formarse con 10 integrantes. Hay seis licenciados, ocho obreros y cinco ingenieros, y en el comité debe haber cuatro licenciados, tres obreros y tres ingenieros. ¿Cuántos comités diferentes pueden formarse?
Se va seleccionar un comité de 4 personas , a partir de un grupo de 7 hombres,dos de los cuales son hermano_cual es la probabilidad de que por lo menos uno de los hermanos esté en el comité?
ResponderEliminarcuantos comites de 5 personas se pueden formar con 8 estudiantes de grado 10 y 4 de grado 11 para que el comite quede conformado por 3 grado 10 y 2 de grado 11
ResponderEliminarcuantos comites de 5 personas se pueden formar con 8 estudiantes de grado 10 y 4 de grado 11 para que el comite quede conformado por 3 grado 10 y 2 de grado 11
ResponderEliminarMe pueden ayudar ?
ResponderEliminarMi problema es cuántos directivos de 3 miembros (presidente secretario y tesorero) se pueden formar de un grupo de 8 elegibles
ResponderEliminarde cuantas maneras se pueden formar un comite de 4 personas elegidas de un grupo de 6 hombres y 6 mujeres. si el comite debe. contener mas hombres que mujeres
ResponderEliminarayuden porfavor