PROBABILIDAD

1.-Se lanza un dado.

a) Encontrar el espacio muestral. Solución: S = {1, 2, 3, 4, 5, 6}

b) Enumerar los puntos muestrales. Solución: Hay seis puntos muestrales: {1},{2},{3},{4},{5} y {6}.

c) Poner dos ejemplos de eventos. Solución: evento A = {resultado es impar} = {1, 3, 5}; evento B = {resultado es mayor que 2} = {3, 4, 5, 6}

d) ¿Son mutuamente excluyentes los siguientes eventos? A = {resultado menor o igual a 4}, B = {resultado es primo}. Solución: A = {1, 2, 3, 4} y B = {2, 3, 5} sí tienen dos puntos en común, 2 y 3. Por lo tanto, no son mutuamente excluyentes.

e) ¿Cuál suceso es complementario a M = {2, 6}? Solución: {1, 3, 4, 5}.

f) ¿Son dependientes o independientes los siguientes eventos? A = {obtener un 2 un el primer lanzamiento}, B = {obtener un 4 en el segundo lanzamiento}. Solución: Son independientes, porque obtener o no un 2 en el primer lanzamiento no afecta el resultado del segundo lanzamiento.

2) En una tómbola hay dos bolitas blancas y tres bolitas negras, ¿cuál es la probabilidad de sacar una blanca y después una negra?
a) Si hay reposición, esto es, después de sacar la primera bolita, ésta se devuelve a la tómbola.
b) Si no hay reposición, esto es, después de sacar la primera bolita, ésta no se devuelve a la tómbola.
a) En este caso los eventos son independientes ya que al reponer la bolita la ocurrencia de un evento no afecta al otro.  Sean los eventos A: "sacar una bolita blanca" y B:  "sacar una bolita negra", entonces, usando:
P(AB)=P(A)•P(B), P(AB)=2/5•3/5=6/25
b) Si no hay reposición, los eventos son dependientes ya que la bolita no es repuesta a la tómbola, por lo que ocupamos:
P(AB)=P(A)•P(B/A)=2/5·3/4=3/10


3) Repita el problema 2) anterior, pero ahora la pregunta es ¿cuál es la probabilidad de sacar una blanca y una negra? (note que ahora no importa el orden).
a) Si hay reposición, esto es, después de sacar la primera bolita, ésta se devuelve a la tómbola
b) Si no hay reposición, esto es, después de sacar  la primera bolita, ésta no se devuelve a la tómbola.
a) Usando la definición, el número total de casos posibles es 5•5=25 y el número de casos favorables es 2•3+3•2=12(una blanca y una negra ó una negra
y una blanca), luego, P(A)=12/25=48%. O bien,
usando las propiedades,
P(A)=P(sacar blanca)•P(sacar después negra)  + P(sacar negra)•P(sacar después blanca)=2/5·3/5+3/5·2/5=12/35=48%
b) Número de casos posibles: 5•4=20 y el número de casos favorables =2•3+3•2=12, luego,
P(B)=12/20=3/5=60%.  O bien, usando las propiedades
P(B)=P(sacar blanca)•P(sacar negra/sabiendo que ha salido blanca) +P(sacar negra)•P(sacar
blanca/sabiendo que ha salido negra) =2/5•3/4+3/5•2/4=3/5=60%

4) Para obtener licencia para conducir, es necesario aprobar tanto el examen teórico como el práctico. Se sabe que la prob. que un alumno apruebe la parte teórica es 0,68, la de que apruebe la parte práctica es 0,72 y la de que haya aprobado alguna de las dos partes es 0,82. Si se elige un alumno al azar, ¿cuál es la prob. de que apruebe el examen para obtener licencia?
Sea A: aprobar la parte teórica, (P(A)=0,68)
Sea B: aprobar la parte práctica, (P(B)=0,72)
Debemos calcular la prob. de A y B, P(AB).
Usando P(AB) = P(A)+P(B)-P(AB), despejamos P(AB):
P(AB)=P(A)+P(B)-P(AB) y reemplazando,
P(AB)=0,68+0,72-0,82=0,58=58%


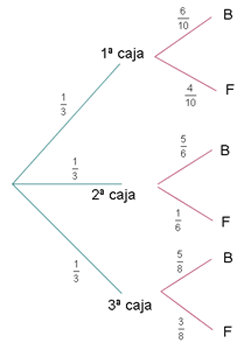
5.-  dispone de tres cajas con bombillas. La primera contiene 10 bombillas, de las cuales a y cuatro fundidas; en la segunda hay seis bombillas, estando una de ellas fundida, y la tercera caja hay tres bombillas fundidas de un total de ocho. ¿Cuál es la probabilidad de que al tomar una bombilla al azar de una cualquiera de las cajas, esté fundida?

 

6. Se extrae una carta de una baraja española de 40 cartas. Si la carta extraída es un rey, nos dirigimos a la urna I; en caso contrario a la urna II. A continuación, extraemos una bola. El contenido de la urna I es de 7 bolas blancas y 5 negras y el de la urna II es de 6 bolas blancas y 4 negras. Halla:
a) La probabilidad de que la bola extraída sea blanca y de la urna II
b) La probabilidad de que la bola extraída sea negra.

7.- En una ciudad el 55% de los habitantes consume pan integral, el 30% consume pan de multicereales y el 20% consume ambos. Se pide:
I) Sabiendo que un habitante consume pan integral, ¿ cuál es la probabilidad de que coma pan de multicereales?
II) Sabiendo que un habitante consume pan de multicereales, ¿cuál es la probabilidad de que no consume pan integral?
III) ¿Cuál es la probabilidad de que una persona de esa ciudad no consuma ninguno de los dos tipos de pan?

Para ver el gráfico seleccione la opción "Descargar" del menú superior
SOLUCION:










8.El equipo directivo de cierta empresa del sector de hostelería está constituido por 25 personas de las que un 60% son mujeres. El gerente tiene que seleccionar a una persona de dicho equipo para que represente a la empresa en un certamen internacional. Decide lanzar una moneda: si sale cara, selecciona a una mujer y si sale cruz, a un hombre.
Sabiendo que 5 mujeres y 3 hombres del equipo directivo no hablan inglés, determina, justificando la respuesta, la probabilidad de que la persona seleccionada hable inglés.

Enunciado

9. ¿se lanzan dos dados correctos. calcular la probabilidad del suceso, los numeros obtenidos no suman 4?

 Probabilidad = Casos Favorables / Espacio muestral
Espacio muestral:
Debemos combinar los valores de cada dado para hallar el espacio muestral, esto se halla de la siguiente forma:
6 x 6 = 36
Casos favorables:
Son todos los casos en que la suma de los dados es diferente de 4, para esto debemos hallar primero en cuantos casos la suma es igual a 4
1+3, 2+2, 3+1
Son 3 casos no favorables, entonces los casos favorables son:
36 - 3 = 33
Ahora vamos con la probabilidad:
P = 33/36 = 11/12
Entonces la probabilidad del suceso es igual a 11/12

10. Hay 87 canicas en una bolsa y 68 son verdes. Si se escoge una, ¿cuál es la probabilidad de que esta sea verde?

Solución:

Divide la cantidad de formas de elegir una canica verde (68) por la cantidad total de canicas (87)

68 ÷ 87 = 0.781609

11. Si yo tengo una canasta llena de peras y manzanas, de las cuales hay 20 peras y 10 manzanas. ¿Qué fruta es más probable que saque al azar de la canasta?

Para este ejemplo tenemos que 30 es el total de frutas en la canasta; es decir los casos posibles. Para calcular la probabilidad de sacar una manzana mis casos favorables son 10 puesto que existen sólo 10 manzanas. Así, aplicando la fórmula obtenemos que:

P(Manzana)=10/30=1/3= 33.3% probable

Calculando igual, la probabilidad de sacar pera es:

P(Pera)=20/30=2/3= 66.7% probable

Como 66.7 es mayor que 33.3 es más probable que saque una pera, pues hay más peras que manzanas en la canasta.

12.